2019ICPC-Shanghai

C. Triple

题意

给三个序列，分别从中选取一个数，输出能够构成一个三角形（线段也算）的方案数。

题解

使用 $FFT$ 减去不符合条件的方案

代码

typedef complex <double> cp;
struct FFT{
    int n, R[N];
    cp a[N], b[N];
    const double pi=acos(-1);
    void init(int bound){    //bound是积多项式的最高次幂
        int L(0);
        for(n=1;n<=bound;n<<=1,L++);
        for(int i=0;i<n;i++)R[i]=(R[i>>1]>>1)|((i&1)<<(L-1)),a[i]=b[i]=0;
    }
    void fft(cp* a, int opt){
        int i, j, k;
        cp wn, w, x, y;
        for(i=0;i<n;i++)if(i>R[i])swap(a[i],a[R[i]]);
        for(i=1;i<n;i<<=1){
            wn=cp(cos(pi/i),opt*sin(pi/i));
            for(j=0;j<n;j+=i<<1)
                for(w=cp(1,0),k=0;k<i;k++,w=w*wn){
                    x=a[k+j], y=a[k+j+i]*w;
                    a[k+j]=x+y, a[k+j+i]=x-y;
                }
        }
        if(opt==-1)for(i=0;i<n;i++)a[i]/=n;
    }
    void run(){
        fft(a,1), fft(b,1);
        for(int i=0;i<n;i++)a[i]*=b[i];
        fft(a,-1);
    }
}fft;
ll ans;
int cnta[N],cntb[N],cntc[N];
void fun(int aa[],int bb[],int c[]){
    for (int i = 0; i <fft.n; i++)fft.a[i]=cp(aa[i]);
    for (int i = 0; i <fft.n; i++)fft.b[i]=cp(bb[i]);
    fft.run();
    ll pre=0;
    for(int i=0;i<=1e5;i++){
        ans-=pre*c[i];
        pre+=fft.a[i].real()+0.1;
    }
}
int tn;
int main() {
    int t,x;
    in(t);
    fft.init(2e5);
    for(int ca=1;ca<=t;ca++){
        for (int i = 1; i <= 1e5; i++)cnta[i]=cntb[i]=cntc[i]=0;
        in(tn);
        ans=1ll*tn*tn*tn;
        if(tn<=1000){
            for (int i = 1; i <= tn; i++){
                in(cnta[i]);
            }
            for (int i = 1; i <= tn; i++){
                in(cntb[i]);
            }
            for (int i = 1; i <= tn; i++){
                in(x);
                cntc[x]++;
            }
            for (int i = 1; i <= 1e5; i++)cntc[i]+=cntc[i-1];
            ans=0;
            for (int i = 1; i <= tn; i++)
            for (int j = 1; j <= tn; j++){
                ans+=cntc[min(100000,cnta[i]+cntb[j])]-cntc[max(0,abs(cnta[i]-cntb[j])-1)];
            }
        }else{
            for (int i = 1; i <= tn; i++){
                in(x);
                cnta[x]++;
            }
            for (int i = 1; i <= tn; i++){
                in(x);
                cntb[x]++;
            }
            for (int i = 1; i <= tn; i++){
                in(x);
                cntc[x]++;
            }
            fun(cnta,cntb,cntc);
            fun(cnta,cntc,cntb);
            fun(cntb,cntc,cnta);
        }   
        printf("Case #%d: %lld\n",ca,ans);
    }
    return 0;
}

D. Counting Sequences I

题意

输入一个 $n$ ，问长度为 $n$ 的数列，满足 $a_1+a_2+\cdots+a_n=a_1\times a_2\times\cdots\times a_n$ 的方案数。

题解

这样的序列满足 $1$ 的数量为 非 $1$ 部分的乘积减去非 $1$ 部分的和，我们只需要枚举非 $1$ 部分就可以了

设序列有 $k$ 种数，每种数有 $c_i$ 个，则方案数为 $\huge C_{n}^{c_1}\times C_{n-c_1}^{c_2}\times\cdots\times C_{n-c_1-\cdots-c_{i-1}}^{c_i}\times\cdots\times C_{c_k}^{c_k}$

代码

ll qPow(ll a, ll b, ll c) {  //求(a^b) % c
    ll ret = 1;
    while (b) {
        if (b & 0x1) ret = ret * a % c;
        a = a * a % c;
        b >>= 1;
    }
    return ret;
}
ll fac[N],inv[N];
ll C(ll a,ll b){
    if(b>a)return 0;
    return fac[a]*inv[b]%mod*inv[a-b]%mod;
}
void init(){//快速计算阶乘的逆元
    fac[0]=fac[1]=1;
    for(int i=2;i<N;i++)fac[i]=fac[i-1]*i%mod;
    inv[N-1] = qPow(fac[N-1], mod - 2, mod);
  	for (int i = N - 2; i >= 0; i--) inv[i] = (inv[i + 1] * (i + 1)) % mod;
}
ll ans[3300];
//总个数，当前的最小值，当前的最小值的个数，总乘积，总和，大于当前最小值的数的贡献
void dfs(int dep,int now,int cnt,ll mul,ll tot,ll w){
    int num1=mul-tot;
    if(dep+num1>3000)return;
    ans[dep+num1]=(ans[dep+num1]+w*C(dep,cnt)%mod*C(dep+num1,num1)%mod)%mod;
    dfs(dep+1,now,cnt+1,mul*now,tot+now,w);//再取一个当前最小值
    for(int i=now-1;i>=2;i--){//取一个更小的值
        dfs(dep+1,i,1,mul*i,tot+i,w*C(dep,cnt)%mod);
    }
}
int main() {
    //freopen("a.txt","w",stdout);
    init();
    for(int i=2;i<=3000;i++){
        dfs(1,i,1,i,i,1);
    }
    int t,n;
    in(t);
    while(t--){
        in(n);
        out(ans[n],1);
    }
    return 0;
}

F. Rhyme scheme

题意

对 $n$ 个元素划分集合，每一种划分对应一个长度为 $n$ 的字符串，对这 $B_n$ 个字符串按字典序排序，问第 $k$ 个是什么。

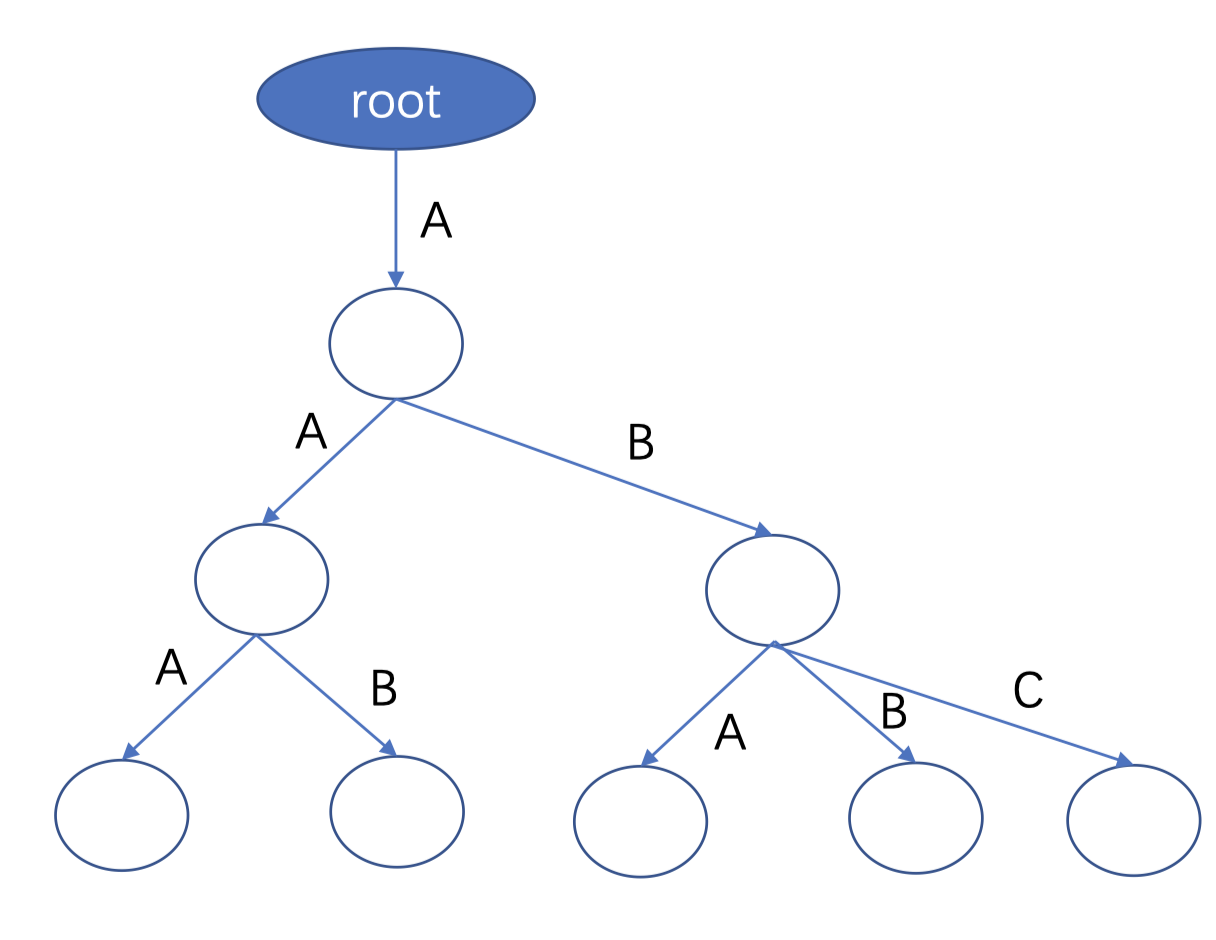
如 $n=3$ 时，字符串为 $AAA,AAB,ABA,ABB,ABC$

题解

设 $dp[n][i][j]$ 表示对于 $n$ 个元素，前 $i$ 个元素被分为了 $j$ 个集合，剩余 $n-i$ 个元素划分集合的方案数。

$$dp[n][i][j]=j*dp[n][i+1][j]+dp[n][i+1][j+1]$$

然后再在字典树上查找答案就可以了

代码

__int128 dp[30][30][30];
int main() {
    for1(i,26){
        for1(j,i)dp[i][i][j]=1;
        for(int j=i-1;j>=0;j--){
            for1(k,j)dp[i][j][k]=k*dp[i][j+1][k]+dp[i][j+1][k+1];
        }
        out(dp[i][1][1]);
        puts("");
    }
    int n,t;
    char s[30];
    in(t);
    for1(ca,t){
        in(n);in(s);
        __int128 k=0;
        for(int i=0,len=strlen(s);i<len;i++){
            k*=10;
            k+=s[i]-'0';
        }
        printf("Case #%d: ",ca);
        int cnt=0;
        for1(i,n){
            for1(j,cnt+1){
                int tm=max(cnt,j);
                if(k<=dp[n][i][tm]){
                    cnt=tm;
                    putchar('A'+j-1);
                    break;
                }else k-=dp[n][i][tm];
            }
        }
        puts("");
    }
    return 0;
}

J. Stone game

题意

$n(1\le n\le300)$ 堆石子，每堆石子有 $a_i(1\le a_i\le 500)$ 个，问有多少种取法使得取走的数量大于等于剩余的数量而且按这种取法丢弃掉任意一堆都将会小于等于剩余的石子数

题解

对石子数从大到小排序， $dp[i]$ 表示总共取 $i$ 的方案数

代码

ll dp[N];
int a[400];
int main() {
    int t,n;
    in(t);
    while(t--){
        in(n);
        ll tot=0;
        for0(i,n)in(a[i]),tot+=a[i];
        sort(a,a+n,greater<int>());
        ll ans=0;
        mem0(dp);
        dp[0]=1;
        int maxx=0;
        for0(i,n){
            maxx+=a[i];
            for(int j=maxx;j-a[i]>=0;j--){
                dp[j]=(dp[j]+dp[j-a[i]])%mod;
                if(2*j>=tot&&2*j<=tot+a[i])ans=(ans+dp[j-a[i]])%mod;//注意加的是dp[j-a[i]]而不是dp[j]，因为dp[j-a[i]]才表示取了a[i]后总和为j的方案数
            }
        }
        out(ans,1);
    }
    return 0;
}